С 2012 года наша организация сотрудничает с Омским Государственным техническим университетом (ОмГТУ) по вопросам математического моделирования транспортных потоков.
ДВУХУРОВНЕВОЕ МОДЕЛИРОВАНИЕ АВТОТРАНСПОРТНЫХ ПОТОКОВ НА ОСНОВЕ КЛЕТОЧНЫХ АВТОМАТОВ И СИСТЕМ С ОЧЕРЕДЯМИ
Д. Ю. Долгушин, В. Н. Задорожный (Омск), С. В. Кокорин (Санкт-Петербург)
Введение
Моделирование дорожного движения с применением теории клеточных автоматов (КА) в течение двух последних десятилетий стало одним из традиционных способов отображения динамики автотранспортных потоков. Модели данного типа позволяют воспроизводить ряд характерных для потоков автомашин явлений, наблюдаемых в действительности: гистерезис скорости при изменении плотности движения, ударные волны, старт-стопное движение и т.п. [1].
Поскольку одним из основных свойств КА является параллельное обновление конфигурации, и новое состояние каждой клетки зависит лишь от ее текущего состояния и состояний ближайших соседей, естественным направлением развития программной реализации сложных моделей на КА является распараллеливание вычислений. Такая реализация моделей дорожного движения позволяет в реальном масштабе времени поддерживать принятие решений при проектировании и реконструкции улично-дорожных сетей (УДС) мегаполисов.
Вместе с тем при решении задач оптимизации больших УДС и их транспортных потоков возможности моделей на КА ограничены. В статье предлагается подход, позволяющий на порядки ускорить решение задач оптимизации за счет совместного использования КА и моделей массового обслуживания.
Имитационная модель дорожного движения на клеточных автоматах
В работе [2] представлена модель, основанная на стохастическом многополосном транспортном клеточном автомате, включающая правила «медленного старта» (slow-to-start) и «пространственного упреждения» (spatial anticipation) [1]. Время в модели дискретно; одна итерация (обновление конфигурации автомата) соответствует одной секунде – среднему времени реакции водителя на изменение дорожной ситуации. Обновление конфигураций ведется по заранее заданному набору правил, определяющему реакцию каждого автомобиля (ускорение, торможение, перестроение) на дорожную ситуацию (наличие выбоин, других машин, сигналы светофора и пр.). Возможность учета эксплуатационного состояния дорожного покрытия и локальных скоростных ограничений, а также включение вероятностного правила «превышения скорости» отличает модель от существующих аналогов (см. их подробный обзор в работе [1]).
На базе данной модели с целью исследования движения транспортных потоков по сети дорог разработана модель УДС [3, 4], ключевым элементом которой является узел. Данный элемент предназначен для связывания дорог и передачи машин между ними. В набор элементов сети дорог также входят: светофор, перекресток (регулируемый и нерегулируемый), пешеходный переход. Использование данных элементов позволяет строить сетевые КА для моделирования УДС с произвольной конфигурацией.
Параллельные вычисления
Имитация индивидуального поведения машин реализуется на КА за счет больших вычислительных мощностей. Для распараллеливания вычислений естественно использовать разделение модели УДС города на модели районов, кварталов, передаваемые разным исполнителям – процессорам, узлам вычислительных кластеров и т.д.
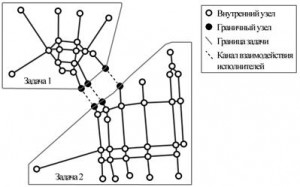
Абстрагируясь от технической реализации многопроцессорной обработки КА, можно сказать, что существует задача, под которой понимается некоторая часть моделируемой УДС (совокупность связанных узлами дорог), которая должна быть передана исполнителю (процессору, узлу кластера). Исполнитель по сигналу некоторого координирующего объекта (координатора), выполняет одну итерацию. По ее выполнении автомобили, достигшие граничных узлов УДС (выходы или входы которых связаны с узлами другой задачи), должны передаваться на соответствующие узлы, принадлежащие другим задачам. На рис. 1 приведен пример модели дорожной сети (центр г. Омска), разделенной на две задачи. Черным цветом на рисунке закрашены граничные узлы.
Рис. 1 Пример разбиения модели УДС на задачи
Программная реализация модели (на примере фрагмента УДС г. Омска, рис. 1) позволяет воспроизводить движение потоков автомашин с его визуализацией в ускоренном режиме на персональном компьютере средней мощности. Приведенный фрагмент включает 45 узлов, соединяющих 170 прямолинейных участков дорог. Начаты работы по реализации параллельной версии модели на вычислительном кластере ОмГТУ.
Уровень сети массового обслуживания
Если оптимизация выполняется в обширном пространстве вариантов, то эффективно реализовать ее можно путем представления УДС в виде сети массового обслуживания (транспортной СеМО), сохраняющей структуру УДС и основные параметры, определяющие вероятностно-временные характеристики (ВВХ) движения транспорта.
Сохраняя «функциональное пространство УДС», транспортная СеМО абстрагируется от пространства физического, учитываемого на уровне КА, и от взаимодействия близко расположенных автомобилей. Двунаправленная дорога представляется в СеМО двумя независимыми дугами, передающими заявки от одних узлов СеМО к другим. Узел СеМО – система массового обслуживания (СМО) – представляет собой место формирования очереди на данном автотранспортном маршруте, т.е. пешеходный переход, перекресток и т.п. Физически единый перекресток разделяется в транспортной СеМО на несколько СМО, лежащих на соответствующих разных маршрутах заявок. Циклическую смену сигналов разрешения и запрета движения через перекресток можно учитывать, задавая в СМО подходящее случайное время x обслуживания заявок. Среднее время обслуживания M(x) должно быть равно среднему времени проезда через перекресток, а дисперсию D(x) можно определять так, чтобы средняя длина очереди в СМО была равна средней длине очереди у перекрестка на данном направлении. Для улучшения качества аппроксимации можно использовать многоканальные СМО.
Особенностью транспортной СеМО является и то, что прохождение заявки от одного ее узла с очередью до другого происходит не мгновенно. На это тратится время, сравнимое со временем прохождения узла с очередью. Чтобы учесть это, каждую дугу, соответствующую дороге, можно представлять в виде СМО с бесконечным (или очень большим) числом каналов, время обслуживания в которых равно времени проезда по этой дороге. Еще одна важная особенность транспортной СеМО состоит в том, что ее переходные вероятности являются функциями известных интенсивностей маршрутов, сливающихся и расходящихся на перекрестках. Если маршрут является пучком маршрутов, т.е. у него имеются альтернативы, характеризуемые вероятностями их выбора, то эти вероятности также влияют на переходные вероятности СеМО.
Представление УДС в виде транспортной СеМО позволяет на два-три порядка ускорить имитационное моделирование (ИМ) и решать оптимизационные задачи. Методы аналитико-имитационного моделирования немарковских СеМО [5-7] позволяют еще на порядки ускорять решение оптимизационных задач и с достаточно хорошей для практических целей точностью оптимизировать СеМО, содержащие сотни узлов.
Пример оптимизации транспортной СеМО
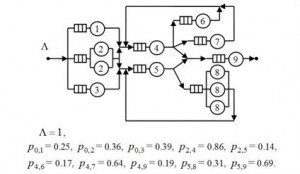
В качестве примера рассмотрим оптимизацию транспортной СеМО, представленной на рис. 2 (для простоты будем считать ее экспоненциальной).
Рис. 2. Пример СеМО, соответствующей некоторому фрагменту УДС
Через сеть проходят пять безальтернативных маршрутов заявок, содержащих циклы (табл. 1). Круглыми скобками обозначена часть цикла, среднее число выполнений которой указано счетчиком nj. Интенсивность входа в сеть заявок j-го безальтернативного маршрута обозначена через aj. Эти маршруты соответствуют маршрутному пассажирскому транспорту. Интенсивность входа в сеть заявок i-го пучка обозначена через Bi. Каждая заявка i-го пучка выбирает его альтернативу j с вероятностью qij.
Таблица 1
|
j |
Безальтернативные |
ai |
ni |
Пучок 1, |
q1j |
Пучок 2, B2 = 0.3 |
q2j |
Пучок 3, B3 = 0.2 |
q3j |
|
1 |
1-4-(6-4)-9 |
0.1 |
2.333 |
1-4-6-4-9 |
0.1 |
1-4-9 |
0.1 |
2-5-8-5-9 |
0.1 |
|
2 |
1-4-(7-4)-9 |
0.1 |
9 |
1-4-7-4-9 |
0.1 |
2-4-9 |
0.1 |
3-5-8-5-9 |
0.9 |
|
3 |
2-4-(6-4)-9 |
0.1 |
2.333 |
2-4-6-4-9 |
0.1 |
2-5-9 |
0.1 |
– |
– |
|
4 |
2-4-(7-4)-9 |
0.1 |
9 |
2-4-7-4-9 |
0.7 |
3-5-9 |
0.7 |
– |
– |
Указанные в табл. 1 параметры СеМО определяют интенсивности заявок на ее дугах и переходные вероятности, значения которых приведены на рис. 2. Формула каждой переходной вероятности представляет собой дробь – отношение суммы интенсивностей маршрутов, проходящих по соответствующей выходной дуге узла, к сумме интенсивностей маршрутов, входящих в узел. Слагаемые в числителе и знаменателе дроби в общем случае являются интенсивностями ai безальтернативных маршрутов (возможно, помноженными на счетчики ni) и интенсивностями bij = qijBi альтернатив.
Среднее время E прохождения заявок через сеть рассчитывается (в общем случае с помощью ИМ) известными методами с учетом интенсивностей обслуживания, очередей и средних задержек pij на дугах (i, j). Для СеМО рис. 1 время E = 340.7 при указанных в табл. 2 задержках pij и интенсивностях обслуживания (каналами узлов)
m1, m2, …, m9, равных 0.31, 0.22, 0.48, 3.60, 0.79, 0.60, 2.31, 0.08, 1.23 соответственно.
Таблица 2
Средние задержки pij на дугах (i, j) в исходном варианте СеМО
|
p01 |
p02 |
p03 |
p24 |
p25 |
p46 |
p47 |
p49 |
p58 |
p59 |
p14 |
p35 |
p64 |
p74 |
p85 |
|
5.71 |
6.10 |
6.21 |
5.92 |
5.13 |
6.61 |
83.3 |
6.94 |
5.55 |
6.41 |
5.71 |
6.21 |
6.61 |
83.3 |
5.55 |
Средние задержки pij на дугах-дорогах определяются с учетом интенсивности движения по ним и фундаментальных диаграмм дорог, дающих зависимость средней скорости движения автомобиля v от плотности k потока (рис. 3, слева).
Рис. 3. Фундаментальные диаграммы, получаемые моделью на КА: слева – зависимость скорости автомобилей от плотности потока, справа – зависимость потока от плотности. Показано изменение диаграмм после замены асфальтового покрытия альтернативным.
При оптимизации сети перераспределяется общий ресурс ее узлов (сумма взвешенных интенсивностей mi), общий ресурс улучшения дорог и вероятности qij выбора альтернатив в пучках. Как показали полевые испытания модели на КА, проведенные в г. Омске, эта модель после ее калибровки характеризуются высокой точностью прогноза времени прохождения автомобилями разнообразных маршрутов. Пример диаграмм на рис. 3 слева, полученных с помощью модели на КА, показывает, что эффект улучшения дороги можно учитывать коэффициентом, входящим в зависимость v(k), определяющую задержки pij. При оптимизации СеМО рис. 1 этот коэффициент допускалось изменять на 20% при сохранении суммы изменений. В результате перераспределения ресурса узлов, распределения ресурса дорог и вероятностей выбора альтернатив показатель E снизился с 340.7 до 187.7, изменились переходные вероятности (в пределах 15%), вероятности q12 и q14 снизились до нуля. Полученный оптимальный вариант распределения ресурса проверен на устойчивость по отношению к эволюционному уравновешиванию средней длительности альтернативных маршрутов каждого пучка. После такого уравновешивания вероятности выбора маршрутов отклонились от оптимальных значений незначительно, и показатель E ухудшился мало (возрос со 187.7 до 188.2).
Двухуровневое моделирование, в котором используются КА и транспортные СеМО, позволяет продолжать оптимизацию за счет возвращения результатов решения задачи на СеМО в модель на КА, уточнения полученного варианта УДС, и, при необходимости, выполнения новых циклов его оптимизации на СеМО и уточнения на КА.
Моделирование подтвердило предположение [8], что в случае невысоких коэффициентов загрузки для адекватного описания потоков в СеМО достаточно их интенсивностей, а с увеличением загруженности дорог требуется учитывать коэффициенты вариации интервалов между заявками.
Транспортная СеМО как агрегирующая модель позволяет быстро рассчитывать и оптимизировать глобальные ВВХ УДС на основе локальных показателей, оцениваемых КА-моделью, т.к. используемые численные методы [5-10] лишь в редких случаях требуют обращаться к ИМ в ходе решения задачи. Большие транспортные СеМО также можно эффективно имитировать с применением параллельных вычислений.
Выводы
Построение дорожных сетей на базе предлагаемого двухуровневого подхода позволяет исследовать возможность и целесообразность реструктуризации УДС, производить оценку схем светофорного регулирования, выделять оптимальные по времени прохождения маршруты движения, прогнозировать распределение автотранспортных потоков по дорожной сети при заданных дорожных условиях, обосновывать требования к точности задания параметров транспортных СеМО и эффективно синхронизировать распределенные имитационные модели как на уровне КА, так и на уровне СеМО.
Литература
1. Maerivoet S., De Moor B. Cellular Automata Models of Road Traffic // Physics Reports. 2005. Vol. 419, no. 1, Pp. 1-64.
2. Долгушин Д. Ю., Мызникова Т. А. Имитационное моделирование дорожного движения для оценки экологического влияния автотранспорта // Системы управления и информационные технологии, 4.1(38), 2009. – С. 139-142.
3. Долгушин Д. Ю., Мызникова Т. А. Компьютерное моделирование движения городского автотранспорта // Материалы 64-й научно-технической конференции ГОУ “СибАДИ” в рамках Юбилейного Международного конгресса “Креативные подходы в образовательной, научной и производственной деятельности”, посвященного 80-летию академии. – Омск: СибАДИ, 2010. Кн. 2 – С. 68-72.
4. Долгушин Д. Ю. Библиотека моделирования автотранспортных потоков “Трафика” // Хроники объединенного фонда электронных ресурсов “Наука и образование”, №12 (19), 2010. URL: http://ofernio.ru/portal/newspaper/ofernio/2010/12.doc (дата обращения: 28.03.2011).
5. Задорожный В. Н. Оптимизация однородных немарковских сетей массового обслуживания // Проблемы управления, 2009. – № 6. – С. 68-75.
6. Задорожный В. Н. Распределение каналов в однородных немарковских сетях с очередями // Омский научный вестник, 2010. – № 1 (87). – С. 5?10.
7. Кокорин С. В., Соколов Б. В. Комбинированный метод оптимизации структуры замкнутых однородных сетей массового обслуживания / Имитационное моделирование. Теория и практика (ИММОД-2009): Материалы 4?й всероссийской конференции. Том 1. – СПб.: ЦТ СС, 2009. – С. 149-151.
8. Кокорин С. В., Рыжиков Ю. И., Автоматический синтез программ расчета систем и сетей обслуживания. СПб: Доклад на конференцию ИММОД, 2009.
9. Рыжиков Ю. И. Машинные методы расчета систем массового обслуживания. СПб: ВИКИ им А. Ф. Можайского, 1979.
10. Kokorin S., Sokolov B., Numerical Methods of Structure Optimization of Homogeneous Queuing Networks Proceeding of the 7th EUROSIM Congress on Modeling and Simulation, 2010, 2, 29.
Долгушин Дмитрий Юрьевич (Сибирская государственная автомобильно-дорожная академия «СибАДИ»).
Задорожный Владимир Николаевич (Омский государственный технический университет – ОмГТУ).
Кокорин Сергей Владимирович (Санкт-Петербургский Институт Информатики и автоматизации РАН – СПИИРАН).
ДВУХУРОВНЕВОЕ МОДЕЛИРОВАНИЕ АВТОТРАНСПОРТНЫХ ПОТОКОВ НА ОСНОВЕ КЛЕТОЧНЫХ АВТОМАТОВ И СИСТЕМ С ОЧЕРЕДЯМИ
Д. Ю. Долгушин, В. Н. Задорожный (Омск), С. В. Кокорин (Санкт-Петербург)
Аннотация
Приводится описание разработанной комплексной модели дорожного движения на основе стохастического многополосного транспортного клеточного автомата. Предлагается концепция двухуровневого моделирования с использованием клеточных автоматов и сетей с очередями для решения задач оптимизации транспортных сетей.
TWO-TIER MODELING OF TRAFFIC FLOW BASED ON CELLULAR AUTOMATON AND QUEUEING SYSTEMS
D. Y. Dolgushin, V. N. Zadorozhnyi (Omsk), S. V. Kokorin (St. Petersburg)
Annotation
The article describes the developed complex model of automobile traffic flow based on stochastic multilane cellular automaton. The concept of road netrowk optimization by means of two-tier modeling involving cellular automaton and queueing models is proposed.
*Исследования проводились при финансовой поддержке РФФИ (проекты № 10-08-00906, № 10?08?90027_Бел-а, 11-08-01016, 11-08-00641, 11-08-00767), ОНИТ РАН (проект 2.3).
УДК 519.2:004.421.5:004.7
В. Н. Задорожный, Е. Б. Юдин
Омский государственный технический университет, г. Омск
Моделирование автотранспортных сетей и потоков:
программные средства и математические подходы
Введение
Задачи, поставленные Транспортной стратегией Российской Федерации до 2030 г. [1], предполагают перевод практики транспортного планирования развития городов, регионов и страны в целом на качественно иной уровень. В соответствии с задачами Транспортной стратегии в России должна быть создана единая интегрированная комплексная сбалансированная транспортная система. Транспортную инфраструктуру России необходимо поднять на качественно новый уровень, сделать ее конкурентоспособной по отношению к лучшим мировым аналогам и обеспечить потребности развития экономики и общества в качественных транспортных услугах.
Решение этих стратегических задач невозможно без математического моделирования транспортных сетей и потоков.
Вместе с тем для их успешного решения необходимо объединить усилия большого числа проектных и научно-исследовательских организаций, предприятий, органов государственной и муниципальной власти, чтобы обеспечить использование достижений современной теории транспортного моделирования на практике. В качестве примера эффективного сотрудничества организаций, принадлежащих разным ведомствам, можно привести опыт внедрения информационно-аналитической системы PTV Vision® VISUM (см. ниже, п. 1) с мощной математической базой теории транспортного моделирования в структуру государственных органов Германии [2]. Использование и развитие транспортной модели происходит циклически в результате постоянного сотрудничества между государственными структурами, частными перевозчиками, учреждениями общественного транспорта и внешними проектными организациями. Городские управляющие органы и учреждения общественного транспорта отслеживают и предоставляют данные по изменениям в транспортной городской автодорожной сети и изменениям движения общественного транспорта. Внешние проектные организации проводят опросы населения, сбор других необходимых данных, проводят расчет транспортного спроса. На этой основе создается интегрированная транспортная модель общественного и индивидуального транспорта, с помощью которой разрабатывается план транспортного развития города, просчитываются различные сценарии развития городской инфраструктуры, вырабатываются, обосновываются и реализуются соответствующие решения.
Обзор программных и математических инструментов транспортного моделирования позволяет увидеть, насколько, с одной стороны, разнообразны и развиты программные средства и математические модели, применяемые для анализа транспортных сетей, и, вместе с этим, насколько далека эта область исследований от завершения, насколько она нуждается в координации усилий разных школ «теоретиков», «практиков» и «управленцев», решающих транспортные проблемы крупных городов.
1. Существующие программные средства
В настоящее время в мире применяется большое число программных пакетов, реализующих микро-, мезо- и макромоделирование (см. ниже, п. 3.3) автотранспортных сетей и потоков. Некоторые из них перечислены в табл. 1.
Таблица 1
Пакеты моделирования транспортных потоков на микро- мезо- и макроуровнях
|
Микромоделирование |
Мезомоделирование |
Макромоделирование |
|
Aimsun, CORSIM, CityTrafficSimulator, DRACULA, DYNASIM, MATSim, Quadstone Paramics, Sidra Intersection, Sidra Trip, SimTraffic, SIAS Paramics, TransModeler, SUMO, VISSIM |
Aimsun, Cube, Dynameq, DynusT, DYNASMART, TRANSIMS, TransModeler |
Aimsun, DYNEV, Emme, OmniTRANS, OREMS, TransCAD, TransModeler, VISUM, CUBE VOYAGER |
В таких коммерческих пакетах как CORSIM (разработка началась более 30 лет назад усилиями Federal Highway Administration), Paramics Modeller (Quadstone Paramics, Великобритания), Aimsun (TSS – Transport Simulation Systems, Испания, Барселона), SimTraffic (Trafficware Corporation, США), PTV Vision (PTV Group, Германия; основные компоненты PTV Vision – программные продукты VISUM и VISSIM) исходный код не доступен для изменения или исследования, и эти пакеты реализованы, как правило, для операционной системы Windows. В таких академических разработках как пакет SUMO (Германия; пакет предназначен для моделирования широкополосных магистралей) исходный код доступен для скачивания, модификации, и существуют версии пакета для ряда популярных операционных систем.
Пакеты микромоделирования транспортных потоков интенсивно развиваются в связи с ростом вычислительных мощностей, возможностей 2D/3D визуализации (рис. 1) и обработки большого количества имеющихся данных, собираемых с миллионов транспортных средств. Это позволяет получать и учитывать данные о скоростях и маршрутах автомобилей.
Пакеты для мезо- и макромоделирования позволяют решать такие задачи как планирование транспортной инфраструктуры и общественного транспорта, графическая обработка сети, анализ и оценка транспортных сетей, прогноз эффекта запланированных мероприятий, создание платформы для транспортных информационных систем.
 Рис. 1. Скриншот экрана демонстрационной версии Paramics Demo
Рис. 1. Скриншот экрана демонстрационной версии Paramics Demo
2. Возможности пакетов моделирования транспортных потоков
Многие пакеты, поддерживающие микромоделирование, позволяют создавать транспортные схемы и накладывать их на карты (такие карты служат фоновыми изображениями, на которые наносятся транспортные сети городов). Особо следует выделить в этой области возможности пакета Aimsun (рис. 2). В большинстве пакетов для микромоделирования существует возможность устанавливать максимальную и минимальную скорость движения, типы дорожных участков, их пропускную способность и т.д.
 Рис. 2. Скриншот экрана демонстрационной версии Aimsun
Рис. 2. Скриншот экрана демонстрационной версии Aimsun
В табл. 2 представлены результаты сравнения известных пакетов, полученные независимыми исследователями. Детальные обзоры существующих пакетов моделирования транспортных сетей и потоков можно найти в [3, 4].
Таблица 2
Результаты сравнения пакетов моделирования
|
Авторы |
Пакеты |
Выводы |
|
Middelton, Cooner, 1999 |
CORSIM (FRESIM component), FREQ and INTEGRATION |
Пакеты исследовались для моделирования движения транспорта на автостраде. Все пакеты показали адекватные результаты для исследуемой задачи. Установлено также, что исследуемые пакеты не могут быть использованы для моделирования в условиях перегруженности движения. |
|
Barrios и др, 2001 |
CORSIM, VISSIM, PARAMICS, SimTraffic |
Пакеты оценивались на основе возможностей визуализации (анимации). В частности, пакеты тестировались для моделирования движения автобусов. В конечном счете, выбор авторов остановился на пакете VISSIM, поддерживающем широкие возможности 3-D визуализации транспортных потоков. |
|
Trueblood, 2001 |
CORSIM, SimTraffic |
Результаты обзора показали небольшое различие между системами при моделировании магистралей с низким и умеренным трафиком. Статья устанавливает необходимость детального анализа моделей и важность процедуры валидации моделей. |
|
Demmers и др., 2002 |
CORSIM, SimTraffic |
Исследовались возможности моделирования перегруженной основной магистрали (одной для всех систем). |
|
Kaskeo, 2002 |
VISSIM, CORSIM, SimTraffic |
При моделировании сравнивались три типа объектов: автострады, развязки и магистрали с согласованием сигналов. Сделан вывод, что CORSIM является самым зрелым и широко используемым пакетом, а VISSIM – наиболее мощным и универсальным. Исследование показало также, что VISSIM обладает наименее дружественным интерфейсом и при его использовании требуются дополнительные усилия для пост-обработки результатов. SimTraffic оказался самым простым в использовании. |
|
Bloomberg и др., 2003 |
CORSIM, VISSIM, INTEGRATION, PARAMICS, MITSIMLab, WATSIM, |
Все шесть систем исследовались на основе возможностей их использования при моделировании регулируемых перекрестков и автострад. Исследование показало, что все модели дают адекватные результаты. |
|
Hardy, Wunderlich, 2007 |
30 пакетов, включая VISSIM, Cube, HEADSUP, ETIS, OREMS, Paramics PCDYNEV, TransCAD, TRANSIMS |
В обзоре исследуются возможности пакетов при исследовании чрезвычайных ситуаций, моделировании планов эвакуации. Двадцать восемь пакетов используются для планирования эвакуации на уровне макромоделирования. Из пакетов, не относящихся к макромоделированию, рекомендуется пакет CUBE. |
3. Математические подходы
3.1. Классы математических моделей. Можно выделить три основных класса математических моделей, применяемых для анализа транспортных сетей и потоков [5]:
– прогнозные модели объема транспортных корреспонденций между потокопорождающими объектами;
– модели динамики транспортных потоков;
– оптимизационные модели.
Все разнообразие оптимизационных моделей, применяемых для транспортных сетей и потоков, зиждется либо на применении известных классических моделей, являющихся частью теории графов, либо на результатах исследования прогнозных моделей и моделей динамики транспортных потоков, и далее рассматриваться не будет.
3.2. Прогнозные модели. Прогнозные модели предназначены для нахождения ответа на вопрос, в каких объемах и куда будут происходить перемещения (транспорта, грузов, пассажиров или пешеходов). При этом считаются известными расположение потокопорождающих объектов (мест проживания, работы, культурно-бытового обслуживания и т.д.), «статические» характеристики транспортной сети, соединяющей эти объекты, и поведенческие факторы (предпочтения) различных категорий населения. При помощи прогнозных моделей определяют, какими будут усредненные характеристики транспортных потоков в этой сети – объемы межрайонных передвижений, интенсивности потоков на дорогах, распределение автомобилей и пассажиров по путям движения и др.
В качестве формальной основы прогнозных моделей используется так называемый транспортный граф [5], узлы которого соответствуют перекресткам и станциям внеуличного транспорта, а дуги – сегментам улиц и линий внеуличного транспорта. В составе транспортного графа выделяется маршрутный граф общественного транспорта, узлами которого являются остановочные пункты, дугами – сегменты маршрутов между остановочными пунктами. Узлы-остановки соединены с другими узлами графа дугами-посадками и дугами-высадками. Для моделирования поведения пользователей применяется математический критерий, называемый обобщенной ценой пути. Обобщенная цена пути складывается из обобщенных цен входящих в него дуг, и, возможно, обобщенных цен переходов с дуги на дугу в узлах графа. Факторы различной природы обычно выражаются в обобщенной цене пути в минутах (или в условных минутах). Транспортный граф позволяет описывать потоки и способы выбора путей в сети на разных уровнях детализации, вплоть до перемещений отдельных транспортных единиц, пассажиров и пешеходов.
При моделировании транспортных потоков в сети крупного города обычно выделяют четыре этапа:
– этап 1 – оценка суммарных объемов прибытия и отправления из каждого (условно выделенного) района города;
– этап 2 – расщепление объемов по способам передвижения (пешим, на общественном транспорте, на личном транспорте и т.д.);
– этап 3 – определение матриц корреспонденций, определяющих объем передвижений между каждой парой выделенных районов города;
– этап 4 – распределение корреспонденций по путям в транспортной сети, выбираемым участниками движения.
Все перечисленные этапы взаимообусловлены как прямыми, так и обратными связями, что приводит к необходимости решать задачу последовательными приближениями, повторяя шаги в итеративном режиме. При этом задачи каждого этапа решаются раздельно для разных классов пользователей транспортной сети, выделяемых по достаточно очевидным и понятным признакам, после чего результаты раздельного решения задач могут объединяться.
Этап 1 выполняется с учетом пространственного размещения потокопорождающих объектов, подвижности населения, имеющихся демографических и социально-экономических данных, а также результатов специальных обследований, и в основном предшествует собственно математическому моделированию.
Этап 2 – расщепление объемов прибытия в районы и отправления из них по способам передвижения – выполняется на основе разделения пользователей на классы. Это позволяет учитывать дополнительную информацию о предпочтениях пользователей разных классов, определяющих выбор ими способов передвижения и путей передвижения.
На этапе 3 для каждого класса пользователей рассчитывается своя матрица корреспонденций. К числу наиболее распространенных моделей, используемых на этом этапе, относятся гравитационные модели, энтропийные модели, модели конкурирующих возможностей и некоторые другие (например, модели конкурирующих центров, модели конкурирующих возможностей Стауффера и др.). Эти модели, как правило, основаны на достаточно простых эвристических предположениях, а в получаемые на их основе расчетные формулы предусмотрительно включаются некоторые неопределенные функции для «настройки» (калибровки) моделей по имеющимся эмпирическим данным. После выполнения настройки применение моделей сводится к выполнению простых алгоритмов [5], что позволяет включать задачи по расчету матриц корреспонденций в вузовские учебники для студентов [6].
Математическое обеспечение этапа 4 – этапа определения объемов движения по путям транспортной сети – представляет собой хорошо разработанный, разветвленный набор моделей и методов, характеризуемых разными возможностями, меняющимися в широком диапазоне, и, соответственно, разной сложностью. Эти модели и методы реализуют нормативный (нацеленный на поиск системного оптимума) или дескриптивный (определяющий результат пользовательской оптимизации маршрутов) подход к определению загрузки путей. Данные модели и методы могут применяться для расчета загрузки путей в случае стационарных (статические модели) или нестационарных (динамические модели) транспортных потоков. Наиболее хорошо обоснованными, развитыми и широко используемыми моделями загрузки путей являются:
– модель равновесного распределения потоков, основанная на принципе Вардрупа;
– расширенные модели равновесного распределения;
– модель оптимальных стратегий.
Суть принципа Вардрупа состоит в следующем: при равновесном распределении загрузки ни один из участников движения не может изменить свой путь так, чтобы уменьшить свою индивидуальную цену поездки. Наиболее простыми моделями, основанными на принципе Вардрупа, являются статические модели. Их достаточно подробное описание приводится, например, в [5]. Расширенные модели равновесного распределения применяются для расчета загрузки путей (для нескольких классов пользователей) в случае переменного спроса на поток, в случае стохастического поведения пользователей, или в случае нестационарных транспортных потоков. Численные методы расчета загрузки в последних двух случаях требуют применения суперкомпьютеров или вычислительных систем с большим числом параллельных процессоров.
Модель оптимальных стратегий описывает выбор маршрутов поездок пассажирами общественного транспорта и используется для определения его загрузки. При расчете загрузки используется подробный транспортный граф, включающий маршрутный граф общественного транспорта.
В общем случае при расчете загрузки путей транспортной сети прогнозные модели должны каким-то образом учитывать зависимость цены путей, выбираемых пользователями, от загрузки этих путей. Зависимость цены пути (например, зависимость времени поездки по данному пути) от его загрузки рассчитывается с помощью моделей динамики транспортных потоков, использующих в качестве исходных данных результаты применения прогнозных моделей. Возникающая при этом петля обратной связи (для определения загрузки путей нужно знать их цену, а для определения цены – загрузку) решается путем итеративного поочередного применения прогнозных моделей и моделей динамики транспортных потоков.
По этому поводу важно сделать следующее замечание. Модели динамики транспортных потоков дают достаточно простые устойчивые решения в случае малой загрузки дорог (свободное движение при избыточном ресурсе). Однако решения для случая высокой плотности потоков чрезвычайно чувствительны к малейшим флуктуациям параметров дорог и особенностей поведения участников движения. Заторы при высоких плотностях движения могут возникать как будто из ничего. Кроме того, сами модели динамики транспортных потоков еще далеки от совершенства и нередко в целях получения хотя бы каких-то решений используют явно нереальные предположения. Поэтому в настоящее время, когда возможность применения экстенсивных путей для решения транспортных проблем городов практически исчерпана, углубление теории и моделей динамики транспортных потоков становится насущной необходимостью.
3.3. Модели динамики транспортных потоков. Математические модели и компьютерные программы для моделирования транспортных потоков принято подразделять по уровню детализации объектов моделирования на три крупные категории, относящиеся к микро- мезо- и макроуровням моделирования.
На микроуровне явно выписываются уравнения движения для каждого автомобиля. Транспортные средства рассматриваются как индивидуальные сущности, обладающие своими характеристиками и поведением. Здесь преобладают модели «разумного водителя», в которых ускорение каждого автомобиля описывается как некоторая функция от его скорости, расстояния до впереди идущего автомобиля и скорости относительно лидера [5, 7].
На мезоуровне (так называемые кинетические модели) отдельно взятые машины не моделируются, но учитываются поведенческие особенности водителей. К этому уровню относятся, например, кластерные модели [5, 8], оперирующие группами автомобилей, движущихся с приблизительно одинаковой скоростью на небольшом расстоянии друг от друга, и модели, использующие вероятностные распределения автомобилей как по координате, так и по индивидуальной скорости.
На макроуровне транспортная сеть рассматривается как единое целое, а потоки автомобилей – как потоки сжимаемой жидкости с мотивацией [6, 9].
Как правило, модели динамики транспортных потоков формулируются на языке дифференциальных уравнений (включая уравнения в конечных разностях). Называя такие модели «аналоговыми», Ф. Хейт в [10] противопоставляет им модели теории массового обслуживания (ТМО) и выражает глубокое убеждение, что именно модели ТМО, а вовсе не аналоговые модели, наиболее перспективны в теории транспортных потоков.
Но в теории транспортных потоков за последние полвека широкое развитие получили и «аналоговые» модели, и модели ТМО [6, 11, 12]. Вместе с тем, до сих пор можно наблюдать несколько предвзятое отношение приверженцев разных математических школ к методам и моделям школ «конкурирующих». Так, в конце великолепного обзора [5] при рассмотрении одной из простейших моделей транспортного потока, сформулированных на языке клеточных автоматов (КА), и анализа ее недостатков делается вывод о наличии серьезных теоретических недостатков подхода КА в целом. Заметим, однако, что с чисто теоретических позиций язык клеточных автоматов эквивалентен языку дифференциальных уравнений. На наш взгляд, при исследовании столь сложных явлений, как транспортные потоки, следует искать возможности эффективного синтеза разнообразных математических подходов, руководствуясь тем, насколько эти подходы или их комбинации позволяют продвинуться в решении наиболее актуальных теоретических и практических задач транспортного моделирования.
Применение моделей и методов ТМО при всей их очевидной адекватности задачам анализа транспортных потоков значительно затрудняется ограниченными возможностями аналитического аппарата ТМО. Возможности аналитического решения типичных для ТМО задач резко усложняются или исключаются в тех случаях, когда приходится иметь дело с непуассоновскими потоками заявок, с неэкспоненциальным временем обслуживания заявок в элементах сети, с разного рода априорными зависимостями между состояниями ее элементов и т.д. Выход из этих затруднений на пути применения ТМО мы видим в разработке подходов, комбинирующих аналитические модели и методы с методами имитационного моделирования (или численными методами). Комбинированные аналитико-имитационные модели и методы позволяют успешно преодолевать затруднения, возникающие перед «чисто аналитическим» подходом и эффективно решать весьма широкий круг задач анализа и оптимизации сложных сетей, включая сети с очередями [13-21].
3.4. Комбинированные модели динамики потоков. В научно-исследовательской лаборатории имитационного моделирования, системного анализа и информационных технологий (НИЛ ИМСАИТ) при кафедре АСОИУ ОмГТУ предприняты исследования, направленные на развитие теории транспортных потоков на основе синтеза аналитико-имитационных моделей и методов ТМО с моделями транспортных потоков на КА. Двухуровневая структура разрабатываемой системы распределенного моделирования автотранспортных сетей и потоков должна обеспечивать сокращение времени имитационных экспериментов на порядок и более (по сравнению с одноуровневой структурой). Это имеет большое значение при решении оптимизационных задач и задач многовариантного анализа проектируемых транспортных сетей и проектируемых алгоритмов управления транспортными потоками. Прототип системы должен реализовать «в целом» ее основную концепцию, основанную на следующих положениях:
– за счет использования моделей на уровне КА можно вычислять промежуточные характеристики дорог и транспортных потоков, необходимые для адекватной настройки моделей на уровне сетей с очередями;
– на уровне сетей с очередями за счет применения системы моделирования SimuLab 2 (новой версии системы SimuLab [22]) и разработанных методов оптимизации больших немарковских сетей с очередями [13, 16-20] можно ускорить (на порядки) оптимизацию транспортных сетей и алгоритмов управления транспортными потоками;
– за счет использования специализированной сети ЭВМ НИЛ ИМСАИТ с мощными вычислительными узлами и вычислительного кластера ОмГТУ можно решать сложные практические задачи анализа и оптимизации транспортных сетей и потоков.
В этой системе в основу распределенного моделирования транспортных потоков на КА положена библиотека «Трафика» [23] (на рис. 3 показана визуализация воспроизводимых моделью потоков автомобилей на участке транспортной сети г. Омска). При моделировании можно устанавливать параметры истоков транспортных средств, перекрестков (схемы переключения светофоров, вероятности выбора автомобилями заданных направлений движения), дорожного полотна, указывать пешеходные переходы, а также характеристики транспортных средств (максимальная и рекомендуемая скорость, размер автомобиля). К недостаткам существующей версии программы можно отнести высокую ресурсоемкость, связанную с необходимостью индивидуального моделирования всех транспортных средств и элементов сети. Поэтому лабораторией ИМСАИТ совместно с автором библиотеки «Трафика» разрабатывается ее новая версия, ориентированная на параллельные вычисления (технология MPI), которая позволит моделировать транспортные сети большого размера. Одновременно с этим ведутся работы по созданию редактора моделей, совершенствованию средств визуализации воспроизводимых потоков и средств оптимизации управления транспортными потоками.
Рис. 3. Скриншот экрана программы «Трафика»
В число промежуточных характеристик, вычисляемых на уровне КА, входят фундаментальные диаграммы дорог. На рис. 4. приведен пример из [15] полученных таким образом фундаментальных диаграмм одной из омских дорог.
Рис. 4. Пример фундаментальных диаграмм, получаемых моделью на КА.
Слева – зависимость скорости автомобилей от плотности потока,
справа – зависимость потока q (интенсивности l) от плотности.
Показано изменение диаграмм после замены асфальтового покрытия альтернативным
Обработка результатов моделирования, получаемых на уровне КА, позволяет представить их в форме, удобной для использования на уровне сети с очередями. Например, на рис. 5 показан график аппроксимации фундаментальной диаграммы, представленной на рис. 4 слева, простым алгебраическим выражением зависимости v средней скорости автомобилей от плотности k потока:
Рис. 5. График аппроксимации (белая линия) фундаментальной диаграммы, полученной при моделировании транспортных потоков на уровне КА
Формулы, выражающие зависимость средней скорости v машин от плотности k транспортного потока легко преобразуются в формулы зависимости интенсивности l потока от его плотности. При этом в аппроксимирующие алгебраические выражения могут быть включены коэффициенты, учитывающие чувствительность фундаментальных диаграмм к тем или иным факторам различной природы – к улучшениям поверхности полотна дороги, к изменениям погодных условий, условий видимости и т.д. (рис. 6).
На рис. 7 для сравнения показана диаграмма, приведенная в [6]. Она получена по экспериментальным данным «Центра исследования транспортной инфраструктуры» г. Москвы, собранным (в течение одного дня в 2005 г.) по четырем полосам на участке третьего транспортного кольца от Автозаводской улицы до Варшавского шоссе, и сагрегированные на одну полосу.
Рис. 6. Аппроксимация фундаментальной диаграммы «зависимость интенсивности транспортного потока от плотности». Показаны изменения диаграммы при изменениях коэффициента, учитывающего качество дорожного покрытия
Рис. 7. Пример фундаментальной диаграммы, полученной экспериментально
Разумеется, концепции, положенные в основу разрабатываемой в НИЛ ИМСАИТ двухуровневой системы распределенного моделирования автотранспортных сетей и потоков, учитывают необходимость систематической экспериментальной проверки адекватности реализуемых моделей и методов и необходимость их калибровки по экспериментальным данным. Разные города в разной степени оснащены средствами наблюдения за транспортными потоками. По данным [6], например, в Москве сейчас установлено (в основном на крупных перекрестках) в общей сложности более 500 видеокамер. Порядка 104 -105 автомобилей, курсирующих по Москве и области, оснащены GPS-навигаторами, что позволяет получать треки (пути следования) автомобилей, с информацией о скоростях движения вдоль этих треков. Получение экспериментальных данных и их обработку можно организовать не только путем прямых измерений, но и косвенными методами, например, путем обработки разнообразной текущей документации, которая ведется в организациях и на предприятиях, связанных с транспортом. Это еще раз подчеркивает важность сотрудничества различных организаций при решении транспортных проблем.
Заключение
При разработке и использовании моделей, методов и программных средств моделирования транспортных потоков особое внимание уделяется уровню детализации (грубости) моделей, качеству имеющихся данных, возможностям калибровки и верификации моделей, а также средствам визуального интерфейса.
Наиболее важными для развития теории и практики транспортного моделирования в настоящее время представляются следующие две задачи:
– создание гибридных систем моделирования, позволяющих развивать теорию транспортных сетей и потоков и решать практические задачи путем анализа и оптимизации сетей и потоков сразу на нескольких уровнях детализации;
– развитие приборной составляющей и информационных технологий, обеспечивающих необходимый объем и точность измерений, позволяющих определять характеристики движения транспортных потоков по городским дорогам;
– координация деятельности государственных структур, проектных и научно-исследовательских организаций, учреждений общественного транспорта и частных перевозчиков для решения транспортных проблем крупных городов.
Работа выполнена при поддержке гранта РФФИ 12-07-00149-а.
Библиографический список
1. Транспортная стратегия Российской Федерации, утверждена распоряжением Правительства Российской Федерации от 22 ноября 2008 года № 1734-р; http://mintrans.ru.
2. У. Браннольте, К. Бёттгер, В.Л. Швецов, Ф. Аппельт «Стратегическое планирование транспортной инфраструктуры. Методики проектной оценки в Германии»; ГИС-Ассоциация, «Управление развитием территории» №№ 1,2,3,4 – 2008; http://www.gisa.ru/50526.html.
3. Kotusevski G., Hawick K.A. A Review of Traffic Simulation Software //Technical Report CSTN-095, July 23, 2009.
4. Hardy, M. and K. Wunderlich. Traffic Analysis Tools Volume IX: Work Zone Modeling and Simulation – A Guide for Analysts. Report No. FHWA-HOP-09-001. FHWA, U.S. Department of Transportation, Washington, DC. March 2009.
5. В.И. Швецов. Математическое моделирование транспортных потоков // Автоматика и телемеханика, 2003. – № 11, с. 3-46.
6. Введение в математическое моделирование транспортных потоков: учеб. пособие / Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Н.Б.; Приложения: Бланк М.Л., Гасникова Е.В., Замятин А.А. и Малышев В.А., Колесников А.В., Райгородский А.М; Под ред. А.В. Гасникова. – М. : МФТИ, 2010. – 362 с.
7. Knose W., Santen L., Schadschneider A., Schreckenberg M. Towards a realistic microscopic description of highway traffic // J. Phys. A. Gen.33. 2000. p. 477-485.
8. Hoogendoorn S. P., Bovy P. H. L. State-of-the-art of vehicular traffic flow modeling // Delft University of Technology, Delf, The. 2001 pp. 283-303.
9. Immers L., Logghe S. Traffic floow theory. Curricular Material, May 2002. by Katholieke Universiteit Leuven.
10. Ф. Хейт. Математическая теория транспортных потоков: Пер. с англ. / Под ред. И.Н. Коваленко. – М. : Мир, 1966. – 288 с.
11. Живоглядов В.Г. Теория движения транспортных и пешеходных потоков. –Ростов н/Д: Изд-во журн. «Изв. вузов. Сев.- Кавк. регион», 2005. – 1082 с.
12. Д. Дрю. Теория транспортных потоков и управление ими: Пер. с англ. / Под ред. И.Н. Коваленко. – М. : Изд-во «Транспорт», 1972. – 424 с.
13. Задорожный В.Н. Методы аналитико-имитационного моделирования систем с очередями и стохастических сетей / а-реф. на соиск. уч. ст. д.т.н. по спец. 05.13.18 – Мат. мод-е, числ. методы и комплексы программ. – СПб, 2011. – 36 с.
14. Юдин Е.Б. Методы структурной идентификации больших стохастических сетей и генерации случайных графов в задачах моделирования сложных систем. / а-реф. на соиск. уч. ст. к.т.н. по спец. 05.13.01 – Сист. анализ, упр-е и обр. информации. – Омск, 2012. – 24 с.
15. Задорожный В.Н., Долгушин Д.Ю., Кокорин С.В. Двухуровневое моделирование автотранспортных потоков на основе клеточных автоматов и систем с очередями / Имитационное моделирование. Теория и практика: матер. 5-й Всерос. конф., Т1. – СПб: ФГУП ЦНИИТС.– 2011. – С. 139-144.
16. Задорожный В.Н., Ершов Е.С., Канева О.Н. Двухуровневые градиентные методы для оптимизации сетей с очередями // Омский научный вестник, 2006. – № 7 (43). – С. 119-126.
17. Zadorozhnyi, V.N. Optimizing Uniform Non-Markov Queueing Networks // A simultaneous English language translation of this journal is available from Pleiades Publishing, Ltd. Distributed worldwide by Springer. Automation and Remote Control ISSN 0005-1179. – Vol. 71, No. 6, 2010. – P1158-1169.
18. Задорожный В.Н. Распределение каналов в однородных немарковских сетях с очередями // Омский научный вестник, 2010. – № 1 (84). – С. 5?10.
19. Предпосылки создания фрактальной теории массового обслуживания // Омский научный вестник, 2010. – № 2(90) – С. 182?187.
20. Задорожный В.Н., Тулубаев Д.А. Метамодель систем оперативно-диспетчерского управления сложными крупномасштабными организационно-техническими объектами // Омский научный вестник, 2011. – № 1 (97) – С. 19?23.
21. Юдин Е.Б., Задорожный В.Н. Система агентного моделирования «Simbigraph» / Свидетельство № 2011612193 о государственной регистрации программы для ЭВМ / Федеральная служба по интеллектуальной собственности, патентам и товарным знакам. – М.: РОСПАТЕНТ, – 2011. – № 2011612193.
22. Ершов Е.С., Задорожный В.Н. Комплекс программ оптимизации сетей массового обслуживания «RedOpt» (ОФЭРНиО № 16589) / М.: ИНИМ РАО, ОФЭР «Наука и образование», – 2011. – № 50201150081.
23. Долгушин Д.Ю. Библиотека моделирования автотранспортных потоков «Трафика» // Хроники объедин. ресурсов «Наука и образование», 2010. – № 12.